install.packages(c("tidyverse", "tidymodels", "skimr", "GGally", "ggmap", "kableExtra")) Data Science project with Regression
The following examples are adapted from the excellent book “Hands-on machine learning with scikit-learn, keras and tensorflow” from A. Geron and the tidymodels documentation
In this tutorial you will learn how to specify a simple regression model with the tidymodels package using recipes, which is designed to help you preprocess your data before training your model.
To use the code in this article, you will need to install the following packages:
If you like to install all packages at once, use the code below.
library(tidyverse)
library(tidymodels)
library(skimr)
library(GGally)
library(ggmap)
library(kableExtra)In this example, our goal is to build a model of housing prices in California. In particular, the model should learn from California census data and be able to predict the median house price in any district (population of 600 to 3000 people), given some predictor variables. We use the root mean square error (RMSE) as a performance measure for our regression problem.
Data understanding
In Data Understanding, we first
- Import data
- Get an overview about the data structure
- Discover and visualize the data to gain insights
Import Data
First of all, let’s import the data:
LINK <- "https://raw.githubusercontent.com/kirenz/datasets/master/housing.csv"
housing_df <- read_csv(LINK)Data overview
Next, we take a look at the data structure:
California census top 4 rows of the DataFrame:
head(housing_df, 4)# A tibble: 4 × 10
longitude latitude housing_median_age total_rooms total_bedrooms population
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 -122. 37.9 41 880 129 322
2 -122. 37.9 21 7099 1106 2401
3 -122. 37.8 52 1467 190 496
4 -122. 37.8 52 1274 235 558
# ℹ 4 more variables: households <dbl>, median_income <dbl>,
# median_house_value <dbl>, ocean_proximity <chr>Data info:
glimpse(housing_df)Rows: 20,640
Columns: 10
$ longitude <dbl> -122.23, -122.22, -122.24, -122.25, -122.25, -122.2…
$ latitude <dbl> 37.88, 37.86, 37.85, 37.85, 37.85, 37.85, 37.84, 37…
$ housing_median_age <dbl> 41, 21, 52, 52, 52, 52, 52, 52, 42, 52, 52, 52, 52,…
$ total_rooms <dbl> 880, 7099, 1467, 1274, 1627, 919, 2535, 3104, 2555,…
$ total_bedrooms <dbl> 129, 1106, 190, 235, 280, 213, 489, 687, 665, 707, …
$ population <dbl> 322, 2401, 496, 558, 565, 413, 1094, 1157, 1206, 15…
$ households <dbl> 126, 1138, 177, 219, 259, 193, 514, 647, 595, 714, …
$ median_income <dbl> 8.3252, 8.3014, 7.2574, 5.6431, 3.8462, 4.0368, 3.6…
$ median_house_value <dbl> 452600, 358500, 352100, 341300, 342200, 269700, 299…
$ ocean_proximity <chr> "NEAR BAY", "NEAR BAY", "NEAR BAY", "NEAR BAY", "NE…Data summary of numerical and categorical attributes using a function from the package skimr:
skim(housing_df)| Name | housing_df |
| Number of rows | 20640 |
| Number of columns | 10 |
| _______________________ | |
| Column type frequency: | |
| character | 1 |
| numeric | 9 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| ocean_proximity | 0 | 1 | 6 | 10 | 0 | 5 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| longitude | 0 | 1.00 | -119.57 | 2.00 | -124.35 | -121.80 | -118.49 | -118.01 | -114.31 | ▂▆▃▇▁ |
| latitude | 0 | 1.00 | 35.63 | 2.14 | 32.54 | 33.93 | 34.26 | 37.71 | 41.95 | ▇▁▅▂▁ |
| housing_median_age | 0 | 1.00 | 28.64 | 12.59 | 1.00 | 18.00 | 29.00 | 37.00 | 52.00 | ▃▇▇▇▅ |
| total_rooms | 0 | 1.00 | 2635.76 | 2181.62 | 2.00 | 1447.75 | 2127.00 | 3148.00 | 39320.00 | ▇▁▁▁▁ |
| total_bedrooms | 207 | 0.99 | 537.87 | 421.39 | 1.00 | 296.00 | 435.00 | 647.00 | 6445.00 | ▇▁▁▁▁ |
| population | 0 | 1.00 | 1425.48 | 1132.46 | 3.00 | 787.00 | 1166.00 | 1725.00 | 35682.00 | ▇▁▁▁▁ |
| households | 0 | 1.00 | 499.54 | 382.33 | 1.00 | 280.00 | 409.00 | 605.00 | 6082.00 | ▇▁▁▁▁ |
| median_income | 0 | 1.00 | 3.87 | 1.90 | 0.50 | 2.56 | 3.53 | 4.74 | 15.00 | ▇▇▁▁▁ |
| median_house_value | 0 | 1.00 | 206855.82 | 115395.62 | 14999.00 | 119600.00 | 179700.00 | 264725.00 | 500001.00 | ▅▇▅▂▂ |
Count levels of our categorical variable:
housing_df |>
count(ocean_proximity,
sort = TRUE)# A tibble: 5 × 2
ocean_proximity n
<chr> <int>
1 <1H OCEAN 9136
2 INLAND 6551
3 NEAR OCEAN 2658
4 NEAR BAY 2290
5 ISLAND 5The function ggscatmat from the package GGally creates a matrix with scatterplots, densities and correlations for numeric columns. In our code, we enter the dataset housing_df, choose columns 6 to 9, a color column for our categorical variable ocean_proximity, and an alpha level of 0.8 (for transparency).
ggscatmat(housing_df, columns = 6:9, color="ocean_proximity", alpha=0.8)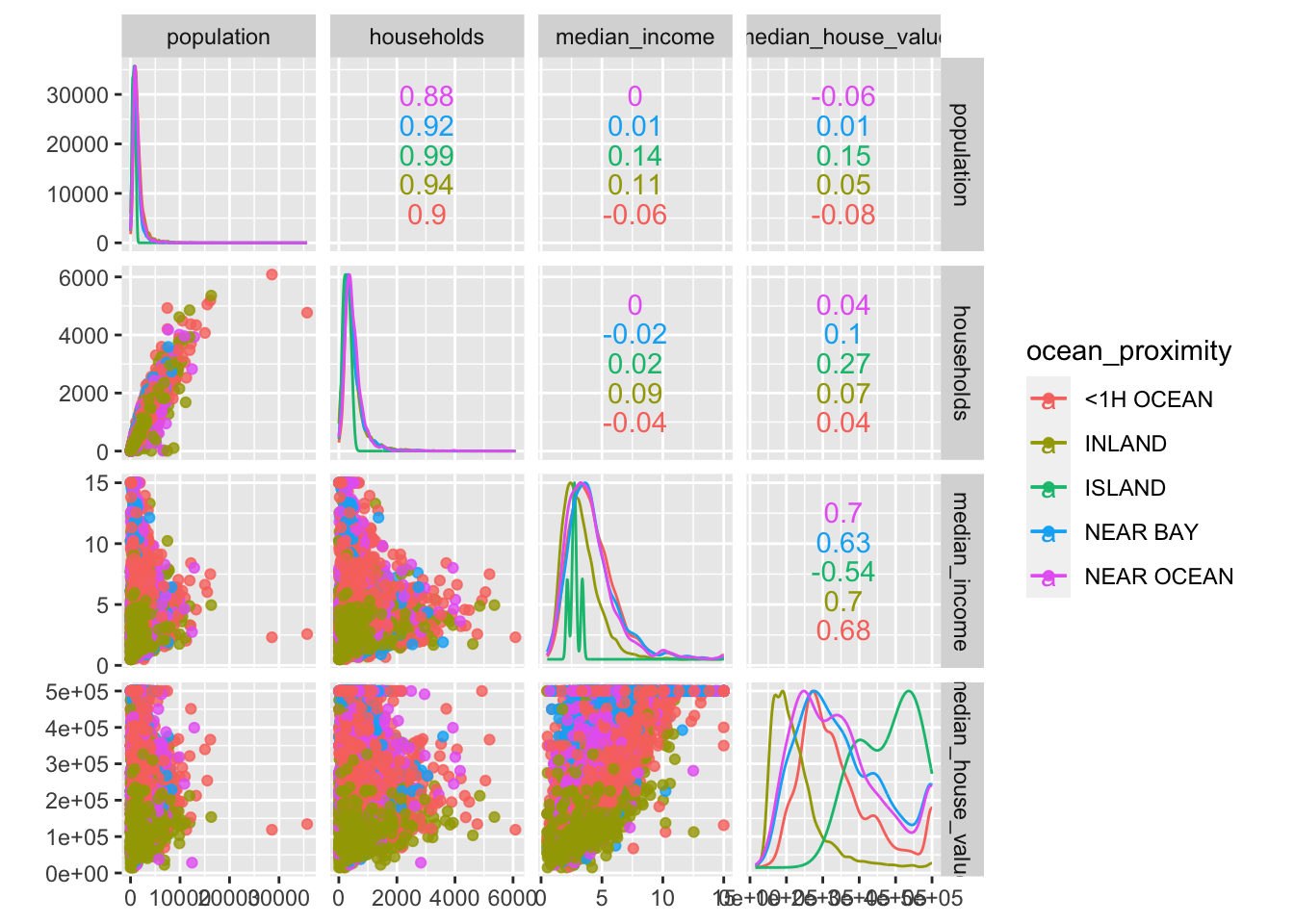
To obtain an overview of even more visualizations, we can use the function ggpairs:
ggpairs(housing_df)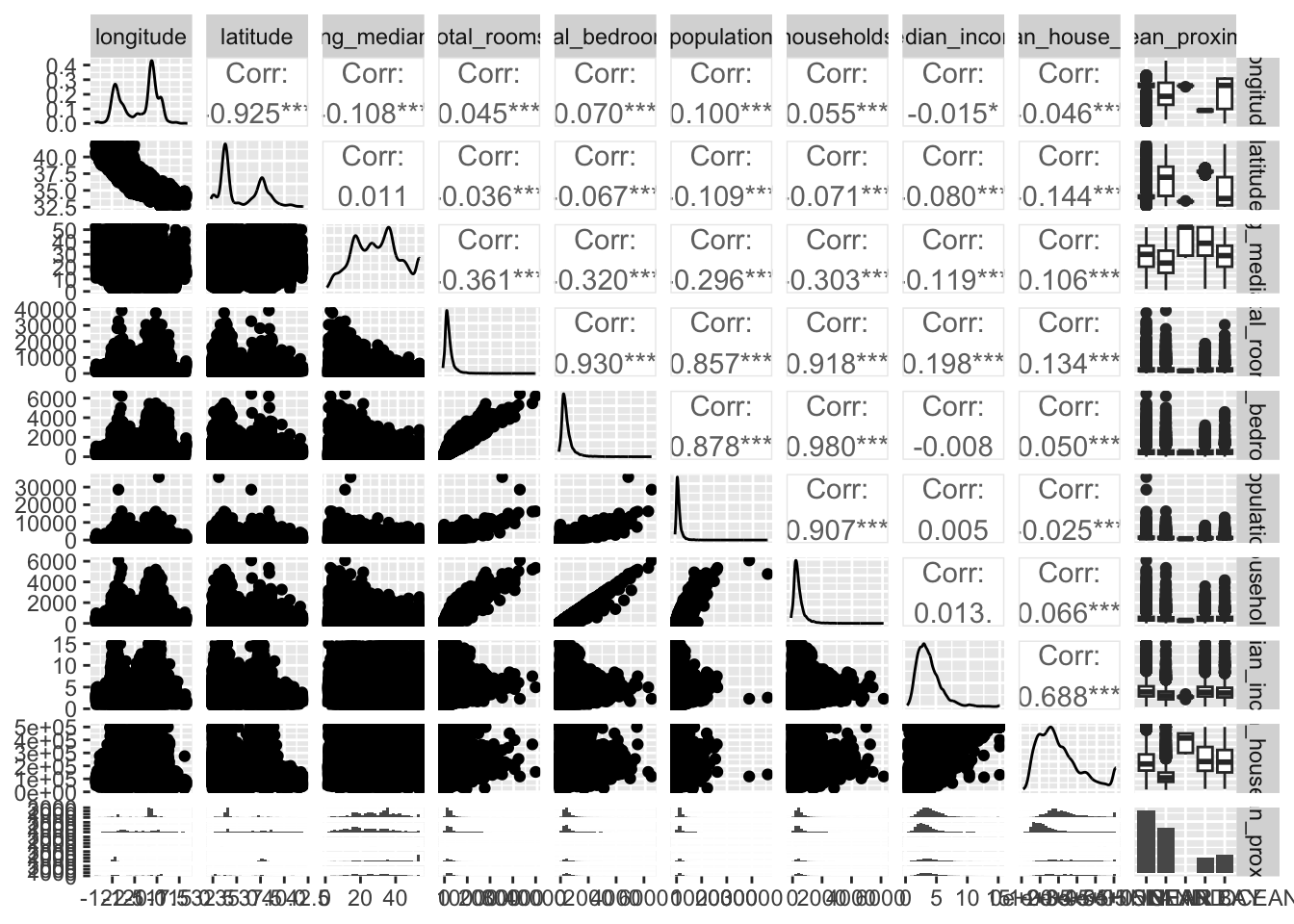
Data exploration
A Geographical scatterplot of the data:
housing_df |>
ggplot(aes(x = longitude, y = latitude)) +
geom_point(color = "cornflowerblue")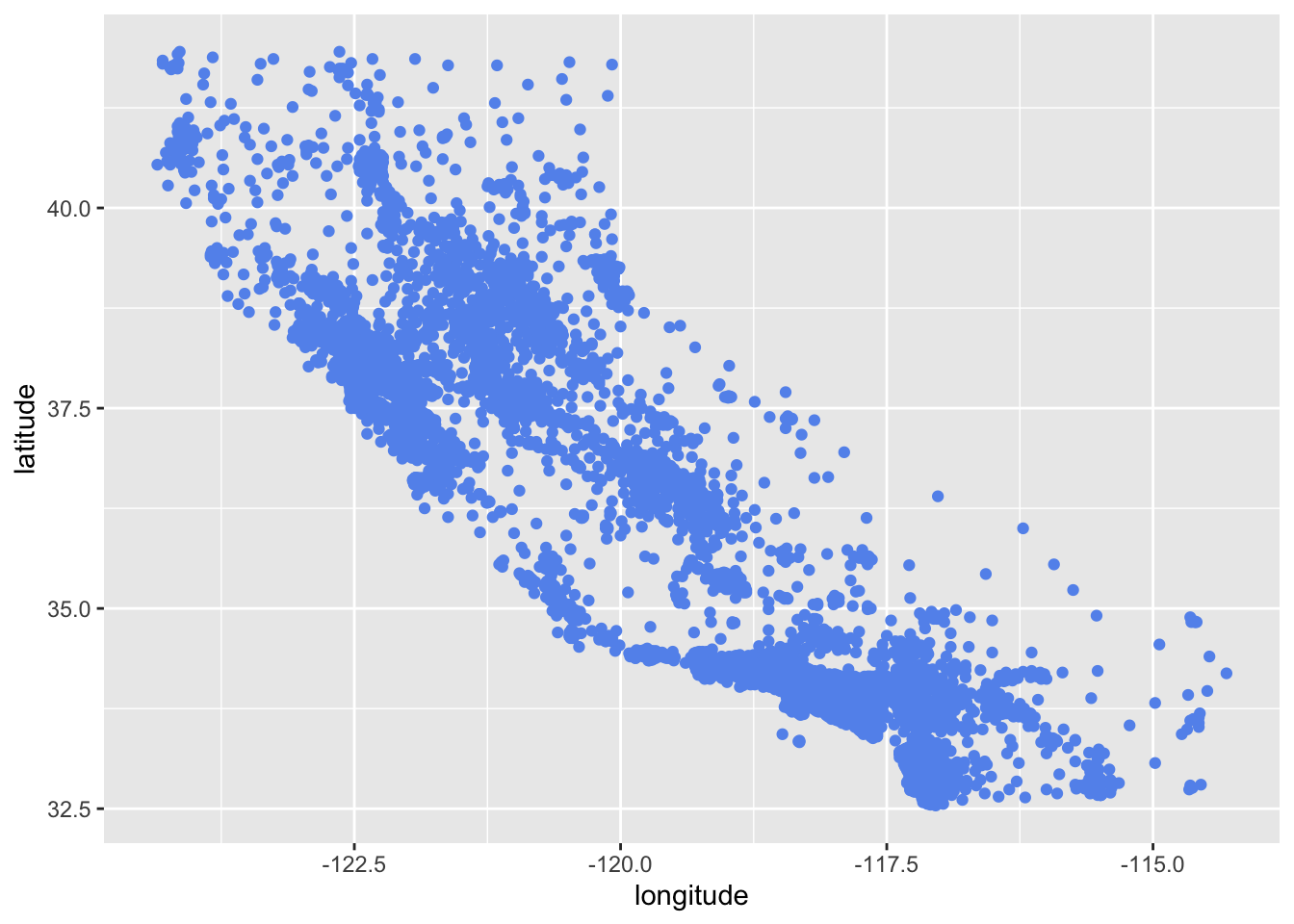
A better visualization that highlights high-density areas:
housing_df |>
ggplot(aes(x = longitude, y = latitude)) +
geom_point(color = "cornflowerblue", alpha = 0.1) 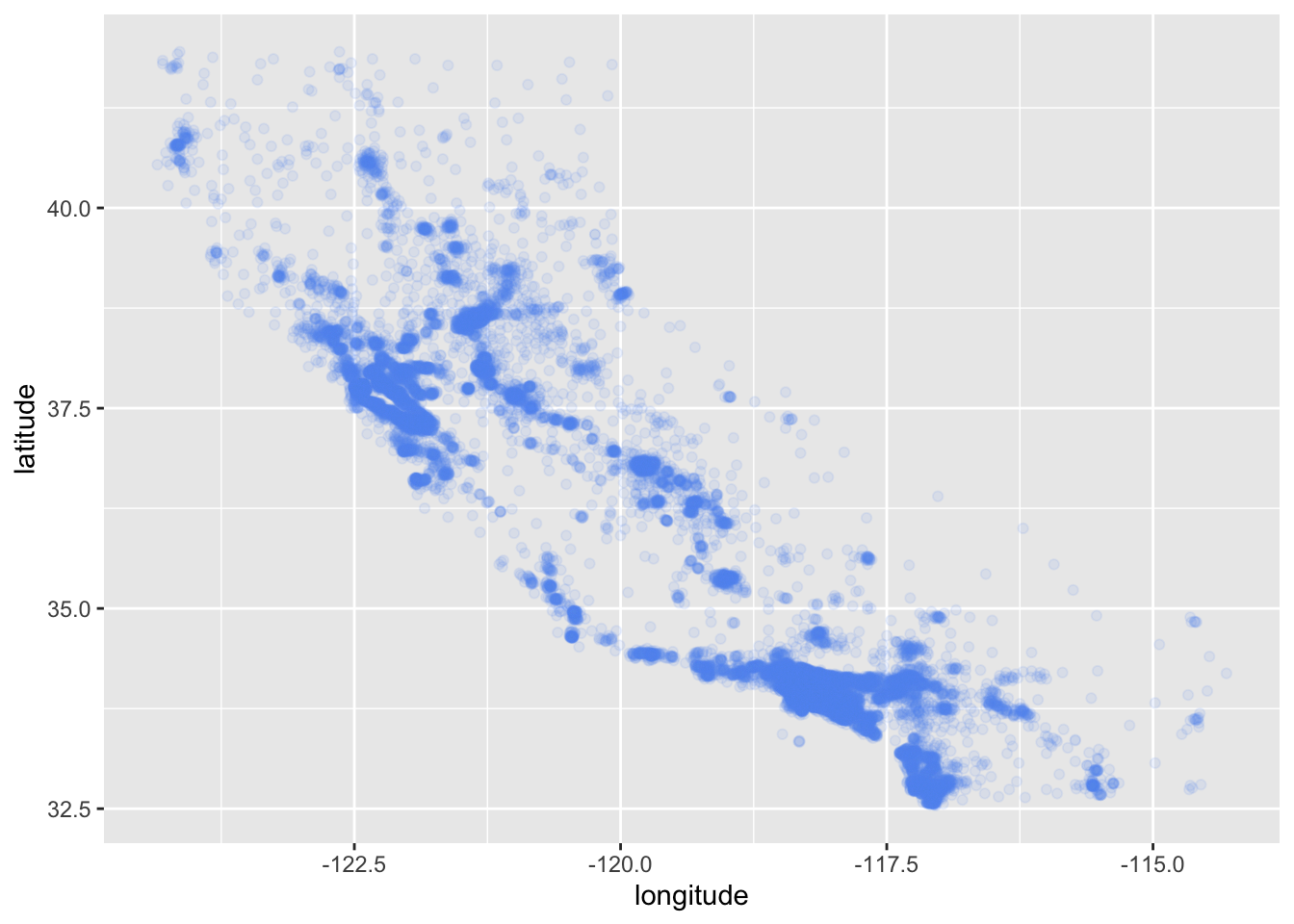
California housing prices:
- red is expensive,
- purple is cheap and
- larger circles indicate areas with a larger population.
housing_df |>
ggplot(aes(x = longitude, y = latitude)) +
geom_point(aes(size = population, color = median_house_value),
alpha = 0.4) +
scale_colour_gradientn(colours=rev(rainbow(4)))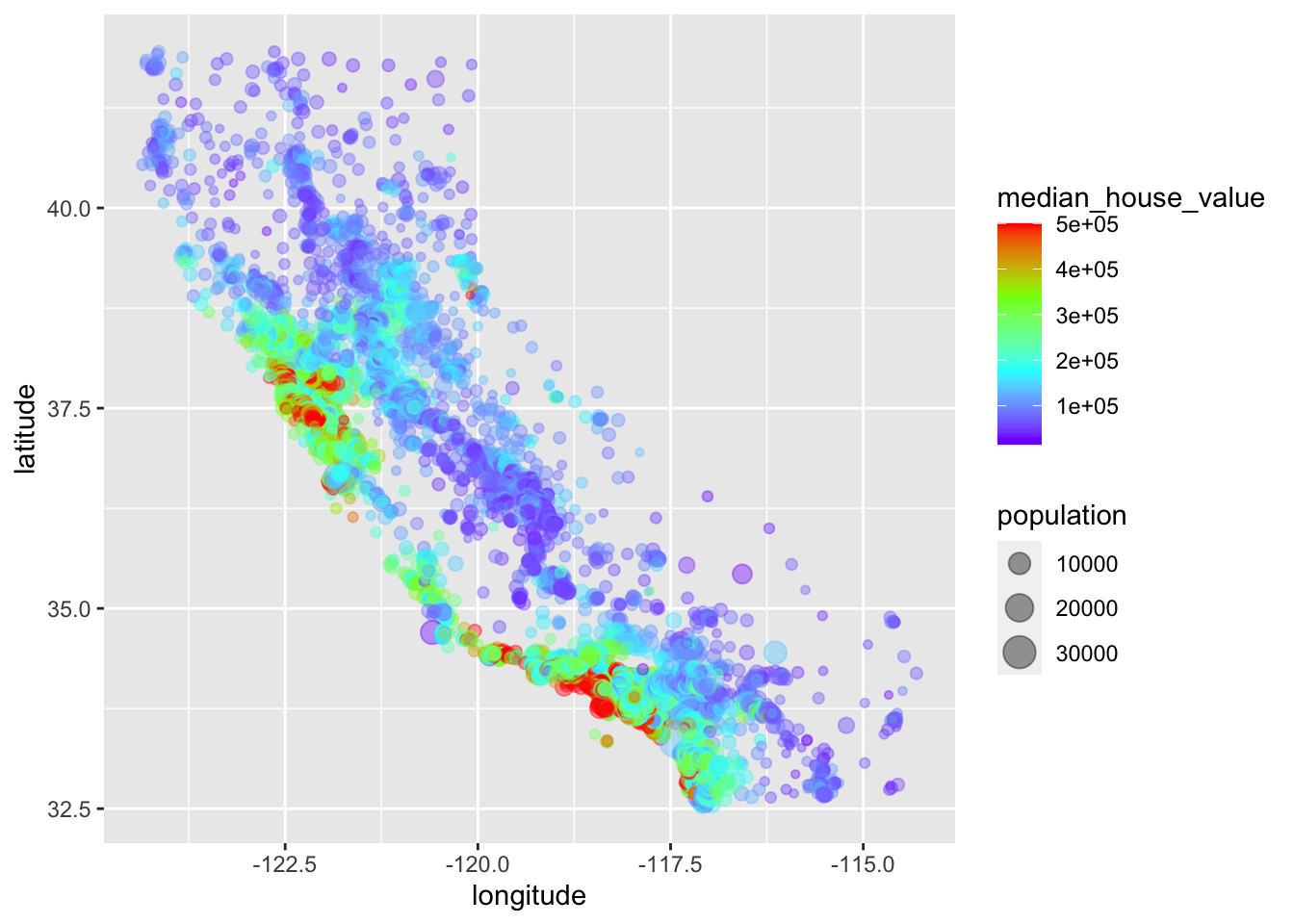
Next, you need to creata a stadiamaps account to display they map.
ggmap::register_stadiamaps("enter-your-AP")library(ggmap)
qmplot(x = longitude,
y = latitude,
data = housing_df,
geom = "point",
color = median_house_value,
size = population,
alpha = 0.4) +
scale_colour_gradientn(colours=rev(rainbow(4)))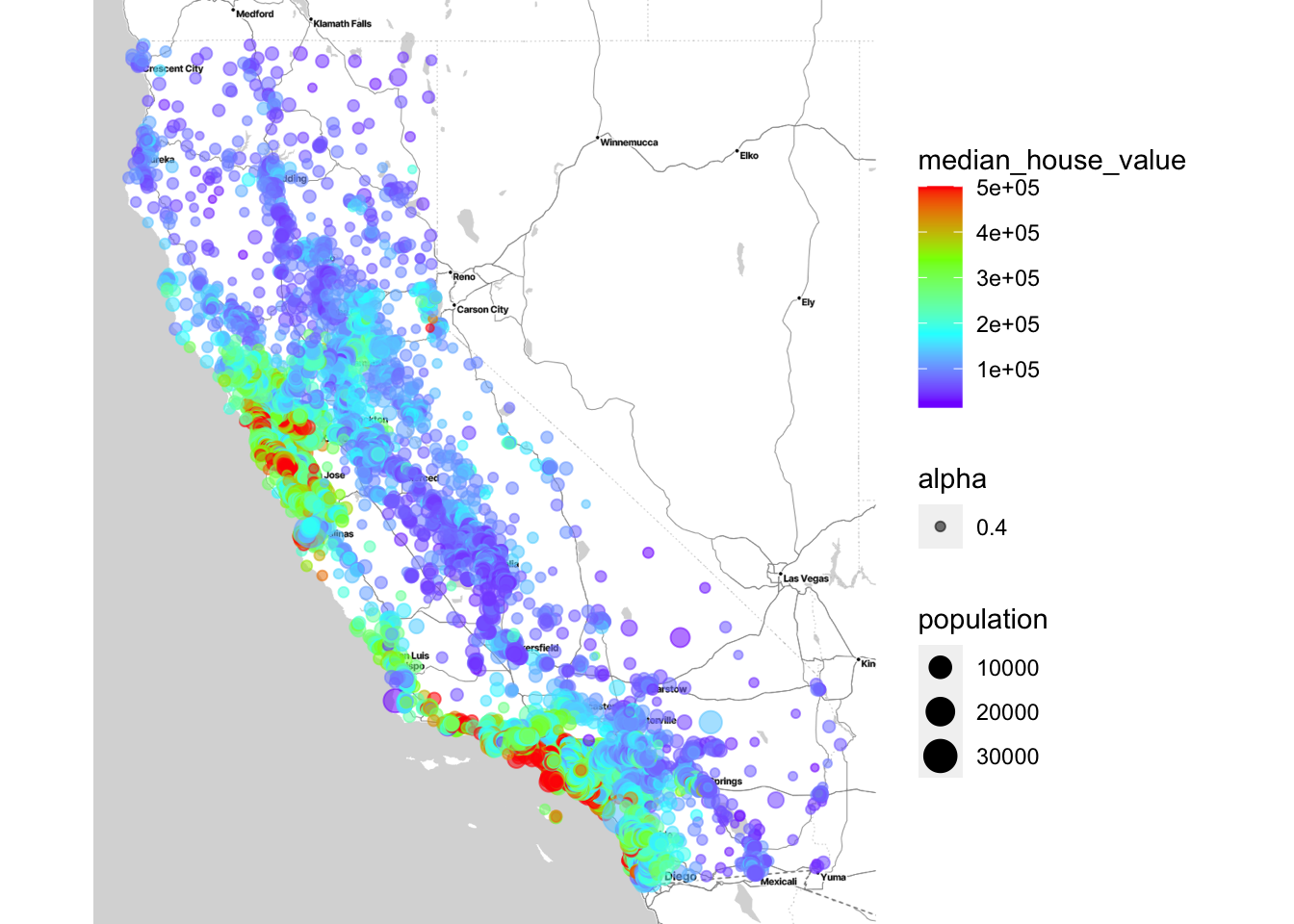
Data preparation
Data splitting
Before we build our model, we first split data into training and test set using stratified sampling.
Let’s assume we would know that the median income is a very important attribute to predict median housing prices. Therefore, we would want to create a training and test set using stratified sampling.
A stratum (plural strata) refers to a subset (part) of the population (entire collection of items under consideration) which is being sampled:
housing_df |>
ggplot(aes(median_income)) +
geom_histogram(bins = 30)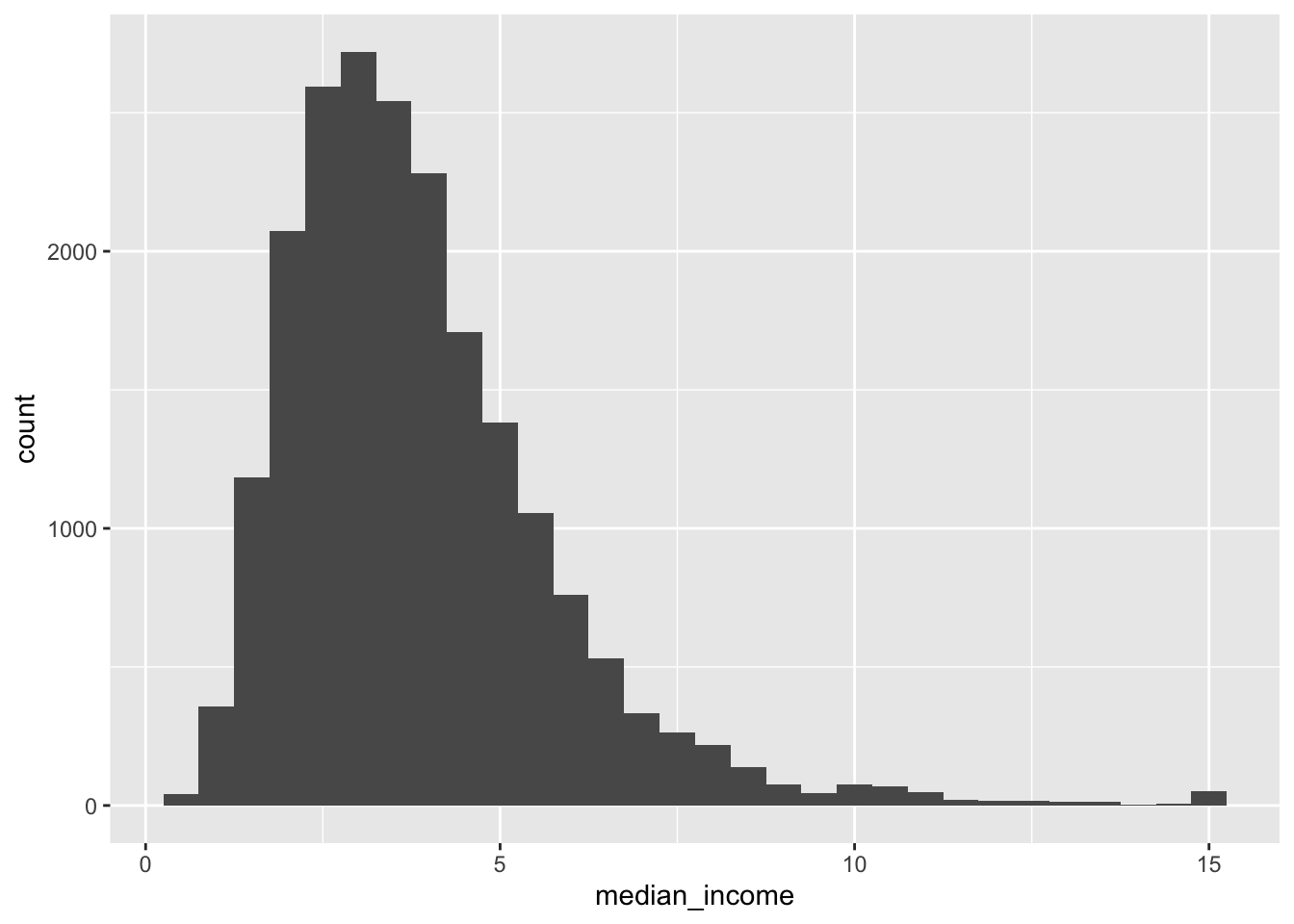
We want to ensure that the test set is representative of the various categories of incomes in the whole dataset. In other words, we would like to have instances for each stratum, or else the estimate of a stratum’s importance may be biased. This means that you should not have too many strata, and each stratum should be large enough. We use 5 strata in our example.
set.seed(42)
new_split <- initial_split(housing_df,
prop = 3/4,
strata = median_income,
breaks = 5)
new_train <- training(new_split)
new_test <- testing(new_split)Recipes
Next, we use a recipe() to build a set of steps for data preprocessing and feature engineering.
Recipes are built as a series of preprocessing steps, such as:
- converting qualitative predictors to indicator variables (also known as dummy variables),
- transforming data to be on a different scale (e.g., taking the logarithm of a variable),
- transforming whole groups of predictors together,
- extracting key features from raw variables (e.g., getting the day of the week out of a date variable),
In summary, the idea of the recipes package is to define a recipe or blueprint that can be used to sequentially define the encodings and preprocessing of the data (i.e. “feature engineering”) before we build our models.
First, we must tell the
recipe()what our model is going to be (using a formula here) and what our training data is.step_novel()will convert all nominal variables to factors.We then convert the factor columns into (one or more) numeric binary (0 and 1) variables for the levels of the training data.
We remove any numeric variables that have zero variance.
We normalize (center and scale) the numeric variables.
housing_rec <-
recipe(median_house_value ~ ., data = new_train) |>
step_novel(all_nominal(), -all_outcomes()) |>
step_dummy(all_nominal()) |>
step_zv(all_predictors()) |>
step_normalize(all_predictors())
# Show the content of our recipe
housing_recNow it’s time to specify and then fit our models.
Model building
Model specification
- Pick a
model type: choose from this list - Set the
engine: choose from this list - Set the
mode: regression or classification
library(tidymodels)
lm_spec <- # your model specification
linear_reg() |> # model type
set_engine(engine = "lm") |> # model engine
set_mode("regression") # model mode
# Show your model specification
lm_specLinear Regression Model Specification (regression)
Computational engine: lm To combine the data preparation with the model building, we use the package workflows.
A workflow is an object that can bundle together your pre-processing, modeling, and post-processing requests
Create workflow
lm_wflow <-
workflow() |>
add_model(lm_spec) |>
add_recipe(housing_rec)Evaluate model
We build a validation set with K-fold crossvalidation:
set.seed(100)
cv_folds <-
vfold_cv(new_train,
v = 5,
strata = median_income,
breaks = 5)
cv_folds# 5-fold cross-validation using stratification
# A tibble: 5 × 2
splits id
<list> <chr>
1 <split [12380/3099]> Fold1
2 <split [12382/3097]> Fold2
3 <split [12384/3095]> Fold3
4 <split [12385/3094]> Fold4
5 <split [12385/3094]> Fold5Now we can fit the model and collect the performance metrics with collect_metrics():
lm_wflow_eval <-
lm_wflow |>
fit_resamples(
median_house_value ~ .,
resamples = cv_folds
)
lm_wflow_eval|>
collect_metrics()# A tibble: 2 × 6
.metric .estimator mean n std_err .config
<chr> <chr> <dbl> <int> <dbl> <chr>
1 rmse standard 69359. 5 549. Preprocessor1_Model1
2 rsq standard 0.643 5 0.00432 Preprocessor1_Model1Usually, we would fit multiple models and select the one with the smallest RMSE. In this example, we only demonstrate the process with one model.
Last fit and evaluation
Fit the best model to the training set and evaluate the test set with the function last_fit():
last_fit_lm <- last_fit(lm_wflow, split = new_split)
# Show RMSE and RSQ
last_fit_lm |>
collect_metrics()# A tibble: 2 × 4
.metric .estimator .estimate .config
<chr> <chr> <dbl> <chr>
1 rmse standard 67113. Preprocessor1_Model1
2 rsq standard 0.651 Preprocessor1_Model1